Sample

1 文本

doc0 = 'Ever tried. Ever failed'

doc1 = 'No matter. Try again.'

doc2 = 'Fail again. Fail better.'

1.1 词－文档矩阵

根据从行还是列的角度来看,可以得到不同的向量

从行来看,可以得到每个词项对应的文档向量

从列来看,可以得到每个文档对应的词项向量

	doc0	doc1	doc2
Ever	2	0	0
tried	1	0	0
failed	1	0	0
No	0	1	0
matter	0	1	0
Try	0	1	0
Fail	0	1	1
again	0	0	2
better	0	0	1

1.2 降维(SVD)

$\begin{matrix} 2&0&0\\1&0&0\\1&0&0\\0&1&0\\0&1&0\\0&1&0\\0&1&1\\0&0&2\\0&0&1 \end{matrix}$ = $\begin{matrix} 0.00&-0.82&0.00\\0.00&-0.41&0.00\\0.00&-0.41&0.00\\0.15&0.00&0.49\\0.15 &0.00&0.49\\0.15&0.00&0.49\\0.52&0.00&0.29\\0.73&0.00&-0.40\\0.36&0.00&0.20\end{matrix}$ $*$ $\begin{matrix}2.53&0&0\\0&2.45&0\\0&0&1.89\end{matrix}$ $*$ $\begin{matrix}0.00&-0.38&-0.92\\-1.00&0.00 &0.00\\-0.00&0.92&-0.38\end{matrix}$

转换后的每一维代表一个潜在概念。（如上矩阵，共有三个潜在概念）

第一个矩阵：每一行代表一个词，每一列表示一个潜在概念，这一行的每个非零元素表示这个词在这个概念中的重要性。如第一个词（Ever）与第二个概念比较相关（－0.82）

第三个矩阵：每一列对应一篇文本，每一行对应一个潜在概念，这一列的每个元素表示这篇文本在不同概念中的相关性。如第一篇文本明显属于第二个概念（－1.00）

因此只要对词－文档矩阵进行一次奇异值分解，就可以同时完成近义词的分类和词的分类

1.2.1 原文档向量和词向量：

doc0 = (2 1 1 0 0 0 0 0 0)^T doc1 = (0 0 0 1 1 1 1 0 0)^T doc2 = (0 0 0 0 0 0 1 2 1)^T

Ever = (2 0 0)^T tried = (1 0 0)^T failed = (1 0 0)^T No = (0 1 0)^T matter = (0 1 0)^T

Try = (0 1 0)^T Fail = (0 1 1)^T again = (0 0 2)^T better = (0 0 1)^T

1.2.2 降维（3维-2维）

取2维德潜在概念

令 令 ＝ 令 ＝

$令U = \begin{matrix}0.00&0.82\\0.00&-0.41\\0.00&-0.41\\0.15&0.00\\0.15&0.00\\0.15&0.00\\0.52&0.00\\0.73&0.00\\0.36&0.00\end{matrix} 令 s ＝\begin{matrix}2.53&0\\0&2.45\end{matrix} 令 V＝ \begin{matrix}0.00&-0.38&-0.92\\-1.00&0.00&0.00\end{matrix}$

1.2.3 新文档向量和词向量

$\overrightarrow{newdoc} = U^T * \overrightarrow{doc}$

$\overrightarrow{newword} = V * \overrightarrow{word}$

1.2.4 计算后结果(LSA)

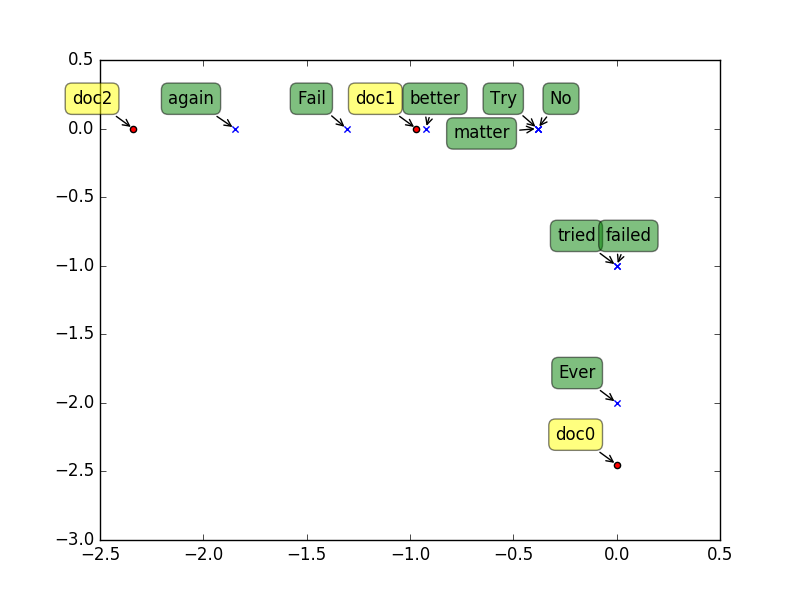
doc0 = (0.00 -2.45)^T doc1 = (-0.97 0.00)^T doc2 = (-2.34 0.00)^T

Ever = (0.00 -2.00)^T tried = (0.00 -1.00)^T failed = (0.00 -1.00)^T No = (-0.38 0.00)^T matter = (-0.38 0.00)^T

Try = (-0.38 0.00)^T Fail = (-1.31 0.00)^T again = (-1.85 0.00)^T better = (-0.92 0.00)^T

这样可以通过新的词向量及文档向量对词或者文档进行分析，如聚类，相似度分析等等。